[시계열 분석]시계열 분석에 필요한 기초 개념

시계열 자료의 기초적인 개념에 대해 알아보겠습니다. R 실습에 필요한 기초적인 개념만 다룰 것이며, 추후 필요한 개념은 따로 정리하겠습니다.

시계열 분석이란?

시간에 따라 관측된 자료(data)를 시계열 자료라고 합니다. 많은 통계 분석 방법들이 데이터 관측값(sample)의 독립성을 가정하고 분석을 진행합니다. 하지만 시간에 따라 관측된 시계열 자료의 경우 관측값들의 연관성을 가지는 경우가 많기 때문에 시계열 분석을 진행하게 됩니다.

시계열 분석 단계는 모델링(Modeling), 예측(Forecasting), 설명(Explanation), 제어(Control)로 크게 4가지로 나눌 수 있습니다. 일반적으로 시계열 분석은 예측에 무게가 실립니다.

시계열 구성요인

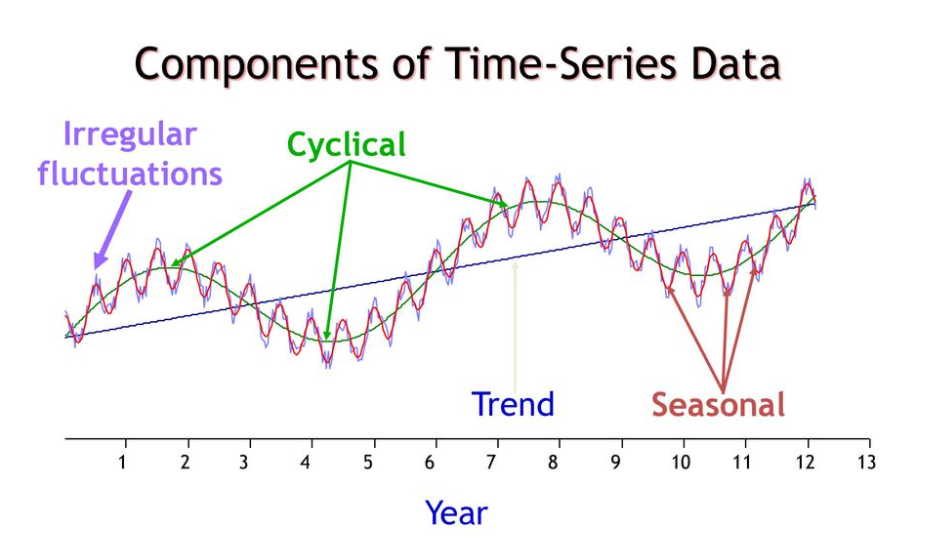
시계열 분석의 모델링 단계는 시계열 자료의 패턴, 즉 시계열 구성요인을 파악하는 것이라 볼 수 있습니다. 그렇다면 시계열 구성요인에는 어떤 것들이 있을까요? 다음과 같이 4가지로 구성됩니다.

1. 추세 요인(Trend Factor)은 인구변동, 인플레이션이나 디플레이션 등의 영향을 받아 시계열 자료에 영향을 주는 장기 변동요인입니다.

2. 순환 요인(Cycle Factor)는 통상적으로 2년에서 10년의 주기를 가지고 순환하는 중기 변동요인입니다. 10년 미만 데이터의 경우 추세 요인과 순환 요인을 구분하기 어렵습니다. 그래서 데이터의 관측기간이 길지 않을 경우 추세 요인으로 묶어 분석하기도 합니다.

3. 계절 요인(Seasonal Factor)은 주로 1년을 주기로 발생하는 변동요인입니다. 추세나 순환에 비해 상대적으로 단기 변동에 해당합니다.(분기나 월을 주기로 가질 수 있습니다.)

4. 불규칙 요인(Irregular Factor)은 측정 및 예측이 어려운 오차변동을 의미합니다. 즉 위의 세 가지 요인으로 설명하고 남은 변동을 의미한다고 보아도 무방합니다.

모형관점에서의 시계열

앞서 설명한 구성요인으로 시계열을 모형화하여 나타낼 수 있습니다. 시계열 구성요인의 결합방법에 따라 가법모형(Additive Model)과 승법모형(Multiplication Model)로 구분합니다.

• 가법모형 : $z_{t}=T_{t}+C_{t}+S_{t}+I_{t}$

• 승법모형 : $z_{t}=T_{t}\times C_{t}\times S_{t}\times I_{t}$
  

  가법모형은 시계열 구성요소가 서로 독립일 경우 사용하며, 승법모형은 구성요소가 상호 의존적인 경우 사용합니다. 승법모형에 log함수를 취하면 가법모형의 형태로 바꿀 수 있기 때문에 주로 승법모형을 사용합니다. 시계열 분석의 관건은 불규칙 요인($I_{t}$)를 얼마나 줄일 수 있는지가 관건입니다.

백색잡음과 확률보행

단변량 시계열 {$z_{t};t=1,\cdot \cdot \cdot ,T$}을 어떤 확률과정(Stochastic Process)의 실현으로 볼 수 있습니다. 확률과정의 가장 단순한 예로 백색잡음과정(White Noise Process)와 확률보행과정(Random walk process)이 있습니다.

1. 백색잡음과정 : $a_{1},a_{2},\cdot \cdot \cdot ,a_{t},\cdot \cdot \cdot$를 평균이 0이고 분산이 $\sigma^2$인 i.i.d.로부터 얻어지는 확률변수라고 할 때, 백색잡음과정은

   $z_{t}=\mu+a_{t},\;\;\; t=1,\cdot \cdot \cdot T,\cdot\cdot\cdot$

   로 정의됩니다. 여기서 $\mu$는 평균 수준을 나타내는 모수입니다. 두 시점 $t$와 ${t}’$의 시차(time lag)를 $k$라고 정의할 때, 자기상관계수는 시점 $t$와 상관없이 $\rho_{k}=Corr(z_{t},z_{t-k})=0$입니다.

2. 확률보행과정 : $a_{1},a_{2},\cdot \cdot \cdot ,a_{t},\cdot \cdot \cdot$를 평균이 0이고 분산이 $\sigma^2$인 i.i.d.로부터 얻어지는 확률변수라고 할 때, 확률보행과정은

   $z_{0}=\mu,\;\;\; z_{t}=z_{t-1}+a_{t},\;\;\; t=1,\cdot \cdot \cdot,$

   로 정의됩니다. 자기상관계수는 $\rho_{t,k}=Corr(z_{t},z_{t-k})=\sqrt{\frac{t-k}{t}}$입니다. 증명은 시점 $t$부터 하나씩 감소하여 모형에 대입하면 쉽게 구할 수 있습니다.

정상성(Stationary)

다음 세 조건을 만족하는 확률과정을 정상시계열이라고 합니다.

1. 평균이 일정.

   즉, 모든 t에 대해 $E(z_{t})=\mu$

2. 분산이 존재하며 상수(constant).

   즉, 모든 t에 대해 $Var(z_{t})=\gamma(0)<\infty$

3. 두 시점 사이의 자기공분산은 시차에만 의존.

   즉, 모든 t와 s에 대해 $Cov(z_{t},z_{s})=\gamma(t-s)$

추세를 갖는 시계열은 조건 1을 만족하지 못하기 때문에 정상시계열의 범주에서 벗어납니다. 또한 변동이 증가하거나 감소하는 경우 조건 2를 만족하지 못하기 때문에 정상시계열이라고 할 수 없습니다. 조건 3을 만족하지 않는 예로는 시계열이 일정한 형태의 반복이 없는 경우가 있습니다. 세 조건을 모두 만족하는 정상시계열은 매우 제한적입니다.

모형평가지표

모형평가지표에는 어떤 것들이 있는지 살펴보겠습니다. 모형평가지표로써 사용되는 함수들은 비용함수(Cost function)이기 때문에 항상 작을수록 좋습니다. 우선 $z_{t}$를 시계열 자료의 관측값, $\hat{z}_{t}$ 을 예측값이라고 하겠습니다.

• ME(Mean Erros) :

$ME = \frac{1}{T}\sum_{t=1}^{T}(z_{t}-\hat{z}_{t})$

• MAE(Mean Absolute Errors) :

$MAE = \frac{1}{T}\sum_{t=1}^{T}\vert z_{t}-\hat{z}_{t} \vert$

• RMSE(Root Mean Square Erros) :

$RMSE = \sqrt{\frac{1}{T}\sum_{t=1}^{T}(z_{t}-\hat{z}_{t})^2 }$

• MPE(Mean Percentage Errors) :

$MPE = \frac{100}{T}\sum_{t=1}^{T}(\frac{z_{t}-\hat{z}_{t}}{z_{t}})$

• MAPE(Mean Absolute Percentage Errors) :

  $MAPE = \frac{100}{T}\sum_{t=1}^{T}\vert \frac{z_{t}-\hat{z}_{t}}{z_{t}} \vert $

어떤 평가지표가 우수한지에 대한 뚜렷한 해답은 없습니다. 따라서 가능한 여러 지표들을 살펴보고 모형 적합도 여부를 결정해야 합니다.