[시계열 분석]R에서 이동평균법(Moving Average Method)과 지수평활법(Exponential Smoothing)
R에서 어떻게 이동평균법(Moving Average Method)와 지수평활법(Exponential Smoothing Method)을 사용하는지 알아보겠습니다. 이 둘을 사용하여 모형적합과 예측은 어떻게 진행되는지도 알아보겠습니다.
이동평균법(Moving Average Method)
평균을 이용하면 불필요한 변동을 줄일 수 있습니다. $Var(X)=\sigma^2$인데 반해, $Var(\bar{X})=\frac{\sigma^2}{n}$임을 생각하면, 평균이 왜 불필요한 변동을 줄일 수 있는지 직관적으로 이해할 수 있습니다. 그렇다면 시계열자료 전체를 평균내어 분석을 진행할까요? 안타깝지만 자료 전체를 평균을 내면 시계열자료의 추세를 반영하지 못합니다.
#install.packages("forecast")
library(forecast)
data("AirPassengers")
plot(AirPassengers, main="AirPassenger")
abline(h=mean(AirPassengers), col="blue")
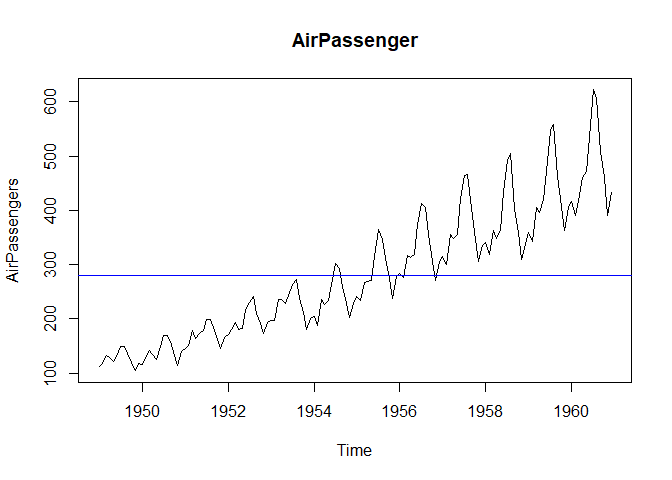
그림에서 볼 수 있듯이 단순 평균은 시계열자료의 추세를 반영하지 못합니다. 따라서 추세를 반영해줄 수 있는 이동평균을 사용해아합니다. 이동평균을 수식으로 나타내면 다음과 같습니다.
N개 자료의 평균을 구했기 때문에 N항 이동평균이라고 불립니다.
위의 과정은 t시점을 기준으로 이전 N개의 자료에 대한 평균을 구한 것입니다. t시점을 기준으로 이전 N/2개와 이후 N/2개 자료에 대한 평균을 구하는 방법도 있습니다. N항 중심이동평균이라고 불리며,
sides=2로 바꿔주면 됩니다.
R에서 N항 이동평균은 어떻게 구하는지 알아보겠습니다.
m3 <- filter(AirPassengers, filter=rep(1/3, 3), sides=1) # 3항 이동평균
m6 <- filter(AirPassengers, filter=rep(1/6, 6), sides=1) # 6항 이동평균
m12 <- filter(AirPassengers, filter=rep(1/12, 12), sides=1) # 12항 이동평균
R의 기본패키지 stats에 있는filter()함수를 사용하면 N항 이동 평균을 구할 수 있습니다. 또한 filter=c()옵션을 사용하면 가중치를 다르게 줄 수 있습니다. 여기서는 N개자료에 동일한 가중치를 주었습니다.
dplyr패키지에서도filter()함수를 제공합니다. 함수명은 같지만 다른 역할을 하므로 중첩을 막기위해패키지명::filter()으로 사용할 수도 있습니다.
par(mfrow=c(2,2))
plot(AirPassengers, main="AirPassengers: original data")
plot(m3, main="3-point moving average")
plot(m6, main="6-point moving average")
plot(m12, main="12-point moving average")
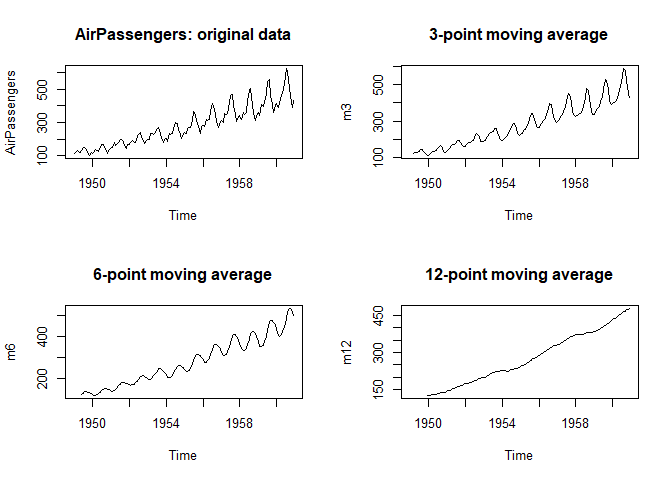
4개의 그림을 비교해보면 항의 수 N이 증가할수록 변동은 줄어들고 추세만 남게됨을 확인할 수 있습니다.
단순이동평균법
$M_t^{(1)}$에서 (1)은 이동평균을 한번 했다는 의미입니다. 이를 단순이동평균(Simple Moving Average)이라고 합니다. 여기서 $M_{t}^{(1)} \cdot \cdot \cdot M_{t-N+1}^{(1)}$를 한번 더 이동평균하게 되면 $M_t^{(2)}$로 나타내고 이중이동평균(Double Moving Average)라고 부릅니다. 우선 단순이동평균을 사용해서 시계열자료를 Smoothing해보겠습니다.
raw_data <- matrix(c(1342, 1442, 1252, 1343, 1425, 1362, 1456, 1272, 1243,
1359,1412, 1253, 1201, 1478, 1322, 1406, 1254, 1289, 1497, 1208))
ts_data <- ts(data=raw_data, start=c(2006,1), frequency=4)
ts_data
## Qtr1 Qtr2 Qtr3 Qtr4
## 2006 1342 1442 1252 1343
## 2007 1425 1362 1456 1272
## 2008 1243 1359 1412 1253
## 2009 1201 1478 1322 1406
## 2010 1254 1289 1497 1208
ts()를 사용하여 4개의 분기를 가지는 시계열 자료로 변환했습니다. 다음으로 filter()를 사용하여 4항 단순이동평균을 구한 후 시각화합니다.
m4 <- filter(ts_data, filter=rep(1/4,4), sides=1)
plot(ts_data, main="ts_data with simple moving average smoothing")
lines(m4, col="red", lty=2, lwd=2)
abline(h=mean(raw_data), col="blue")
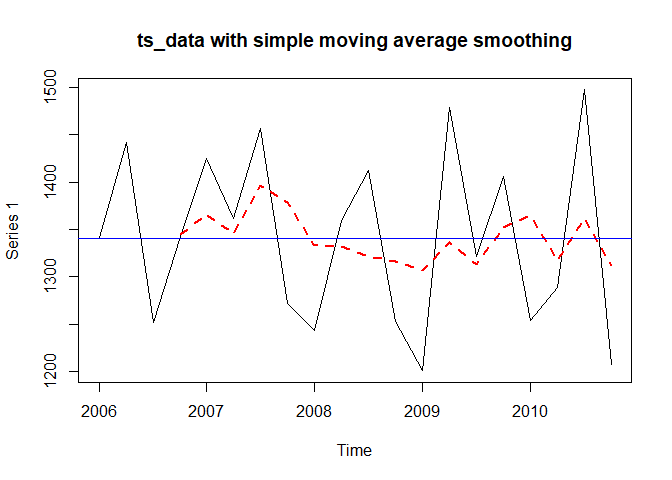
4항 이동평균이기 때문에 4번째 항부터 빨간 점선이 시작됩니다. 원 시계열자료보다 변동이 많이 줄었으며, 추세는 딱히 보이지 않습니다. 다음으로 모형의 잔차가 정상성을 만족하는지 확인해봅니다. tsdisplay()함수는 잔차의 정상성 확인을 위한 그림을 제공합니다.
#remove first three values which are not able to be predicted.
res <- m4[-1:-3,] - ts_data[-1:-3,]
tsdisplay(res, main="Residuals by MA(4) for raw_data")

time plot이 백색잡음형태를 띄고 ACF와 PACF가 파란선을 벗어나지 않는 것으로 보아 정상성을 가짐을 알 수 있습니다. 마지막으로 Box.test()를 통해 잔차가 자기상관성을 가지는지 검정합니다.
Box.test(res, type="Box-Pierce") # H0: Residuals are independent.
##
## Box-Pierce test
##
## data: res
## X-squared = 0.97729, df = 1, p-value = 0.3229
p-value=0.3229로 유의수준 0.05보다 큰 값을 가지므로, “잔차가 독립이다.”(“잔차는 자기상관이 없다.”)라는 귀무가설을 기각하지 못합니다.
이중이동평균법
단순이동평균 $M_{t}^{(1)} \cdot \cdot \cdot M_{t-N+1}^{(1)}$를 다시 이동평균하게 되면 $M_t^{(2)}$로 나타내고 이중이동평균(Double Moving Average)라고 합니다. filter()를 두번 적용하면 이중이동평균을 쉽게 구할 수 있습니다.
m4_1 <- filter(ts_data, filter=rep(1/3,3), sides=1)
m4_2 <- filter(m4_1, filter=rep(1/3,3), sides=1)
plot(ts_data, main="ts_data with Double moving average smoothing")
lines(m4_2, col="red", lty=2, lwd=2)
abline(h=mean(raw_data), col="blue")
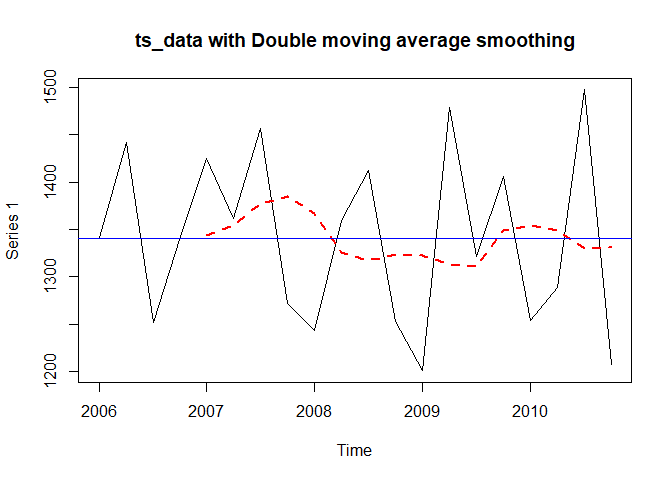
빨간 선이 이중이동평균을 나타낸 그림입니다. 단순이동평균에서보다 더 평활해졌음을 알 수 있습니다. 다음으로 모형의 잔차가 정상성을 가지는지 확인해봅니다.
res2 <- m4_2[-1:-3,] - ts_data[-1:-3,]
tsdisplay(res2, main="Residuals by double MA smoothing")
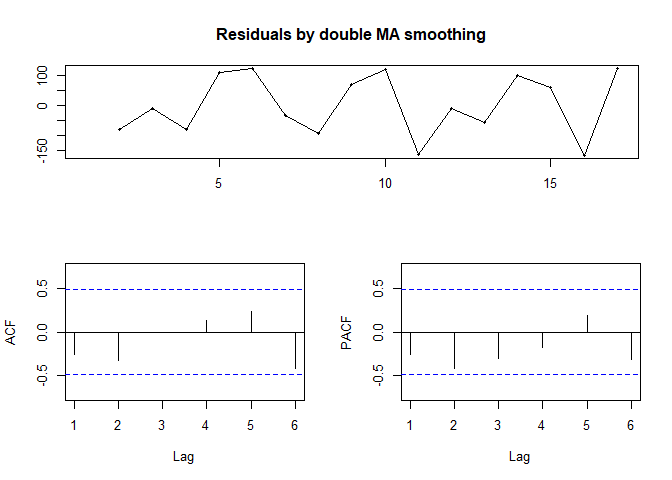
time plot이 백색잡음의 형태를 띄며 ACF와 PACF가 크게 벗어나지 않는 것으로 보아, 잔차가 정상성을 가지는 것으로 보입니다. 마지막으로 잔차의 자기상관성검정을 진행합니다.
Box.test(res2, type="Box-Pierce") # H0: TS is independent
##
## Box-Pierce test
##
## data: res2
## X-squared = 1.0548, df = 1, p-value = 0.3044
p-value=0.3으로 아주 큰 값을 가지므로, “잔차는 자기상관성이 없다.”는 귀무가설을 기각하지 못합니다.
이동평균법을 활용한 시계열 예측
forecast패키지의 ma()를 사용하여도 이동평균을 구할 수 있습니다. order=3은 3항 이동평균을, centre=T는 중심이동평균을 뜻합니다.
mm3_1 <- ma(ts_data, order=3, centre=T) #MA(3) with a center
mm3_2 <- ma(mm3_1, order=3, centre=T) #double MA(3) with a center
$T$시점에서의 이동평균 $M_{T}$은 $T+1$시점의 예측값 $\hat{Y}_{T+1}$이 됩니다. forecast패키지의 forecast함수를 이용하면 시계열자료를 예측할 수 있습니다. 옵션 h=2로 설정하여 이후 2개의 시점 $T+1$, $T+2$를 예측합니다.
f_simple <- forecast(mm3_1, h=2)
f_double <- forecast(mm3_2, h=2)
par(mfrow=c(1,2))
plot(f_simple, main="forecast simple MA(3)") # forecast
plot(f_double, main="forecast Double MA(3)") # forecast
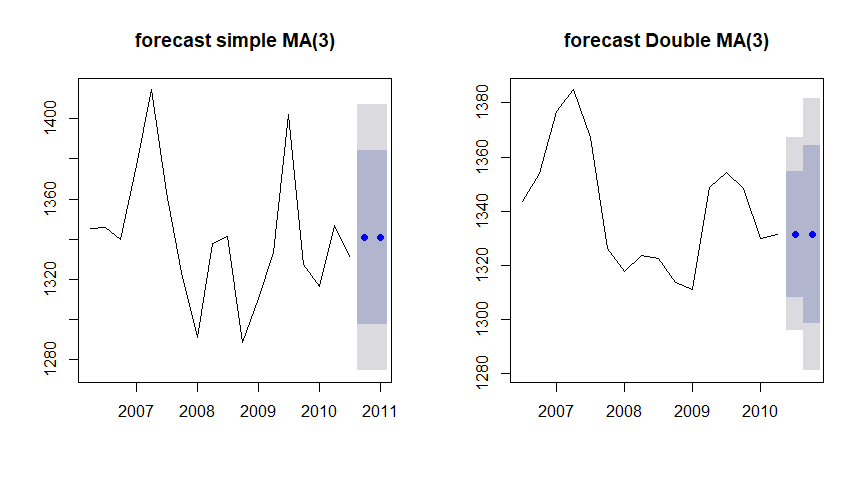
파란 밴드는 80%신뢰구간을, 회색밴드는 95%신뢰구간을 나타냅니다.
f_double
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 2010 Q3 1331.444 1308.163 1354.725 1295.839 1367.049
## 2010 Q4 1331.444 1298.520 1364.368 1281.091 1381.797
accuracy()함수는 모형을 평가하는 여러 지표를 제공합니다.
accuracy(f_double)
## ME RMSE MAE MPE MAPE MASE
## Training set -0.7499552 17.16946 12.23685 -0.06423849 0.9102839 0.4034125
## ACF1
## Training set 0.3147654
지수평활법(Exponential Smoothing Method)
이동평균법과 비교해서 지수평활법은 다음 두 가지 차이점을 가집니다. 하나는 최근값에 더 큰 가중치를 주는 것이고, 다른 하나는 이전 시점의 자료를 모두 사용한다는 것입니다.
단순지수평활법과 이중지수평활법
-
단순지수평활법
$\begin{align} F_{T+1}^{(1)} & = \alpha Y_{T}+(1-\alpha)F_{T}^{(1)} \ & = \alpha Y_{T} + \alpha(1-\alpha)Y_{T-1} + \cdot\cdot\cdot + (1-\alpha)^{T}F_{1}^{(1)} \end{align}$
-
이중지수평활법
$F_{T+1}^{(2)} = \alpha F_{T}^{(1)}+(1-\alpha)F_{T}^{(2)}$
여기서 $\alpha$값은 0과 1사이의 값을 가지는 Hyperparameter로 최적의 값을 찾아야 합니다. 초기추정값 $F_{1}^{(1)}$ 또한 임의로 설정할 수 있지만, 가중치 $(1-\alpha)^T$가 기하급수적으로 감소하기 때문에, 어떤 값을 사용하더라도 모형에 큰 변화는 없습니다.
R에서 HoltWinters()
HoltWinters함수를 사용하면, 알아서 최적의 $\alpha$값을 찾아줍니다. 단순지수평활법을 사용하고 싶다면 beta=F, gamma=F를, 이중지수평활법을 사용하고 싶다면 gamma=F 옵션을 사용하면 됩니다. 여기서는 단순지수평활법을 사용합니다.
ha <- HoltWinters(ts_data, beta=F, gamma=F) #exponential smoothing
ha
## Holt-Winters exponential smoothing without trend and without seasonal component.
##
## Call:
## HoltWinters(x = ts_data, beta = F, gamma = F)
##
## Smoothing parameters:
## alpha: 6.610696e-05
## beta : FALSE
## gamma: FALSE
##
## Coefficients:
## [,1]
## a 1341.998
적합된 모형의 추정치를 출력합니다.
head(ha$fitted, 10)
## xhat level
## 2006 Q2 1342.000 1342.000
## 2006 Q3 1342.007 1342.007
## 2006 Q4 1342.001 1342.001
## 2007 Q1 1342.001 1342.001
## 2007 Q2 1342.006 1342.006
## 2007 Q3 1342.008 1342.008
## 2007 Q4 1342.015 1342.015
## 2008 Q1 1342.010 1342.010
## 2008 Q2 1342.004 1342.004
## 2008 Q3 1342.005 1342.005
plot(ha)
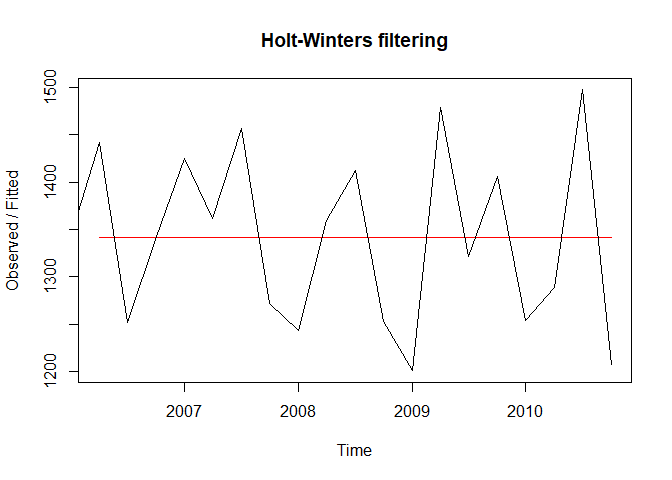
추정값이 거의1342로 동일하여 모형이 수평한 직선을 가지는 것처럼 보입니다. forecast()함수를 사용해 이후 4개의 시점을 예측해봅니다.
f_exp <- forecast(ha, h=4)
f_exp
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 2011 Q1 1341.998 1220.576 1463.421 1156.299 1527.698
## 2011 Q2 1341.998 1220.576 1463.421 1156.299 1527.698
## 2011 Q3 1341.998 1220.576 1463.421 1156.299 1527.698
## 2011 Q4 1341.998 1220.576 1463.421 1156.299 1527.698
plot(f_exp)
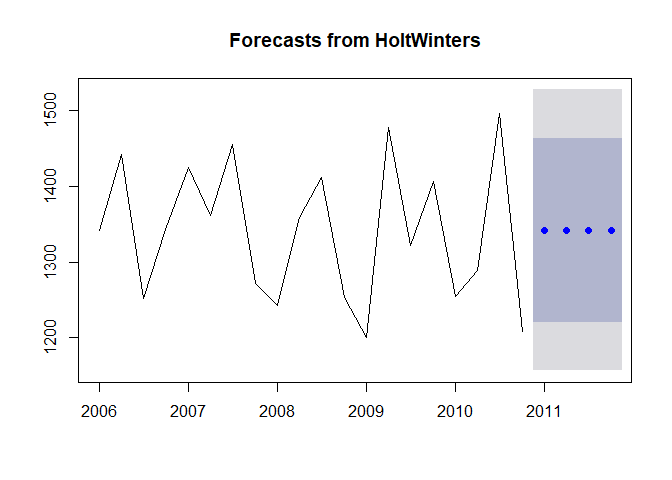
마지막으로 모형의 잔차가 정상성을 가지는지 확인해봅니다.
f_exp$residuals
## Qtr1 Qtr2 Qtr3 Qtr4
## 2006 NA 100.0000000 -90.0066107 0.9993394
## 2007 82.9992733 19.9937865 113.9924647 -70.0150709
## 2008 -99.0104425 16.9961028 69.9949793 -89.0096479
## 2009 -141.0037637 136.0055576 -20.0034333 63.9978890
## 2010 -88.0063417 -53.0005238 155.0029799 -134.0072669
tsdisplay(f_exp$residual)
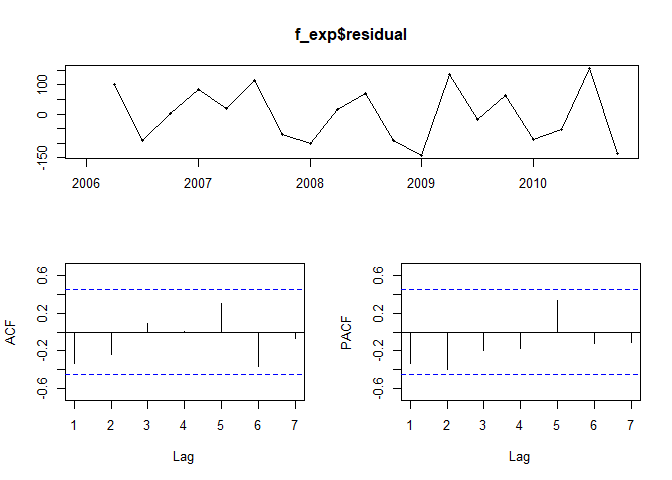
Box.test(f_exp$residual, type="Box-Pierce")
##
## Box-Pierce test
##
## data: f_exp$residual
## X-squared = 2.0761, df = 1, p-value = 0.1496

Leave a comment