[시계열 분석]R에서 tidyverse를 활용한 시계열 분해법(Decomposition)
R의 tidyverse 패키지를 활용해 요소분해법(decomposition)을 진행합니다. 방법론에 대한 자세한 설명은 생략하고, R코드로 어떻게 구현하는지 중점적으로 알아보겠습니다.
분해법이란?
시계열자료는 추세요인, 계절요인, 주기요인, 순환요인으로 총 4가지 요인으로 구성됩니다. 즉, 시계열자료에는 여러 요인들이 중첩되어 있는데, 분해법을 활용하면 이 요인들을 분해할 수 있습니다. 예를 들어, 경제성장은 계절요인과 추세요인이 모두 영향을 미치는데, 만약 장기적인 경제성장을 예측하는게 목적이라면 계절성분을 제거하고 추세성분만 남겨야합니다. 이런 경우 분해법을 진행하면 관심있는 요인인 추세만을 남길 수 있습니다. 또한 분해법을 잔차(Residuals)를 우연변동(Random Variation)에 의한 정상시계열(Stationary Time Series)로 만들 수 있습니다.
우선 시계열분석에 필요한 library를 불러옵니다. R에서 제공하는 기본함수 plot()을 사용하여 시각화할 수 있지만, ggplot2패키지의 autoplot()를 사용하면 더 깔끔한 그래프를 출력할 수 있습니다.
library(tidyverse)
library(ggplot2)
library(forecast)
library(fpp)
library(aTSA)
library(seasonal)
library(timsac)
library(gridExtra)
autoplot(AirPassengers)
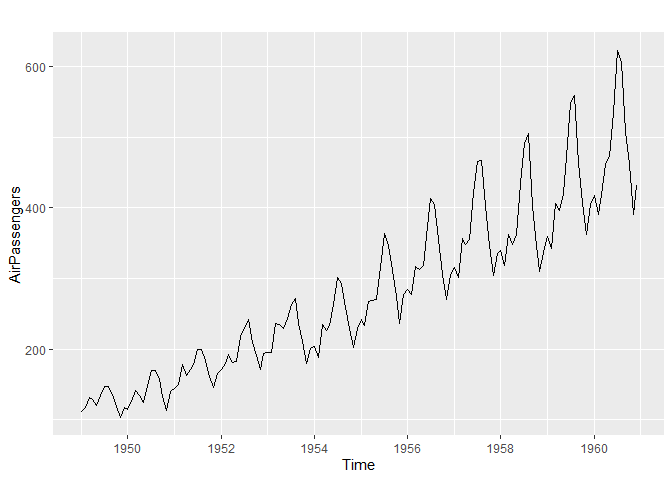
Classical Decomposition
가장 기본적인 분해법이고, 다른 분해법에 비해 상대적으로 절차가 간단합니다. 또한 많은 분해법들이 이 Classical Decomposition을 기반으로 만들어졌습니다. 계절변동이 상수일 때(상수계절변동)와 확률적일 때(이동계절변동) 계절변동 $\hat{S}$을 구하는 과정이 다릅니다. 여기서는 상수계절변동만 다룹니다.
가법분해모형
가법분해모형은 계절변동이 규칙적이고 추세에 의존적이지 않을 경우 적합한 모형으로 $Y_{t}=TC_{t}+S_{t}+I_{t}$ 을 가정합니다. 모형을 분해하는 절차는 다음과 같습니다.
STEP1
이동평균(Moving Average)를 사용하여 추정치 $\hat{TC_{t}}$를 구합니다. 이를 $CMA_{t,d}$(시점 t에서 d개항을 중심이동평균)라고 합니다.
STEP2
$S_{t}+I_{t}$의 추정치 $y_{t}-\hat{TC_{t}}$를 계산합니다.
STEP3
$y_t-\hat{TC_{t}}$ 계열에 대해 계절별로 평균치 $\bar{S_{t}} $를 구한 후, 그 합이 0이 되도록 조정하여 $\hat{S_t}$를 구합니다. 즉, $\hat{S_t} = \bar{S_{t}}-\sum_{t=1}^{d} \bar{S_{t}}/d$를 계산합니다.
STEP4
Remainder component인 $ \hat{R}_t=y_t-\hat{TC}_t-\hat{S}_t $를 계산합니다.
위의 절차를 decompose()함수를 사용하면 쉽게 구할 수 있습니다.
decompose(AirPassengers, type="additive") %>% autoplot()
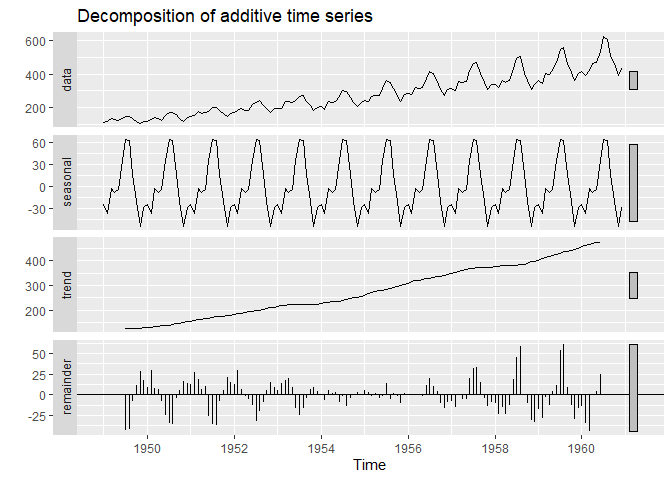
data, seasonal, trend, remainder로 구성된 4개의 plot을 출력했습니다. decompose()가 가지는 values는 다음과 같습니다.
#decomposition
add_decompose = decompose(AirPassengers, type="additive")
add_decompose %>% names()
## [1] "x" "seasonal" "trend" "random" "figure" "type"
#add_decompose$seasonal
#add_decompose$$random
add_decompose$trend
## Jan Feb Mar Apr May Jun Jul Aug
## 1949 NA NA NA NA NA NA 126.7917 127.2500
## 1950 131.2500 133.0833 134.9167 136.4167 137.4167 138.7500 140.9167 143.1667
## 1951 157.1250 159.5417 161.8333 164.1250 166.6667 169.0833 171.2500 173.5833
## 1952 183.1250 186.2083 189.0417 191.2917 193.5833 195.8333 198.0417 199.7500
## 1953 215.8333 218.5000 220.9167 222.9167 224.0833 224.7083 225.3333 225.3333
## 1954 228.0000 230.4583 232.2500 233.9167 235.6250 237.7500 240.5000 243.9583
## 1955 261.8333 266.6667 271.1250 275.2083 278.5000 281.9583 285.7500 289.3333
## 1956 309.9583 314.4167 318.6250 321.7500 324.5000 327.0833 329.5417 331.8333
## 1957 348.2500 353.0000 357.6250 361.3750 364.5000 367.1667 369.4583 371.2083
## 1958 375.2500 377.9167 379.5000 380.0000 380.7083 380.9583 381.8333 383.6667
## 1959 402.5417 407.1667 411.8750 416.3333 420.5000 425.5000 430.7083 435.1250
## 1960 456.3333 461.3750 465.2083 469.3333 472.7500 475.0417 NA NA
## Sep Oct Nov Dec
## 1949 127.9583 128.5833 129.0000 129.7500
## 1950 145.7083 148.4167 151.5417 154.7083
## 1951 175.4583 176.8333 178.0417 180.1667
## 1952 202.2083 206.2500 210.4167 213.3750
## 1953 224.9583 224.5833 224.4583 225.5417
## 1954 247.1667 250.2500 253.5000 257.1250
## 1955 293.2500 297.1667 301.0000 305.4583
## 1956 334.4583 337.5417 340.5417 344.0833
## 1957 372.1667 372.4167 372.7500 373.6250
## 1958 386.5000 390.3333 394.7083 398.6250
## 1959 437.7083 440.9583 445.8333 450.6250
## 1960 NA NA NA NA
처음과 마지막 몇 개의 관측치가 제거되었습니다. Classical Decomposition의 특징 중 하나입니다. 예를 들어서 d=12라면, 처음 6개, 마지막 6개의 관측치가 제거됩니다. 따라서 remainder에서도 관측치가 같이 제거됩니다.
다음은 원 시계열자료에서 계절 및 추세-주기를 제거한 그림입니다. 가법모형을 가정했기 때문에, 단순히 빼주기만 하면 됩니다.
# remove seasonal effects
add_no_seasonal <- AirPassengers - add_decompose$seasonal
# remove trend effects
add_no_trend <- AirPassengers - add_decompose$trend
grid.arrange(
autoplot(add_no_seasonal, main="Additivity model without seasonal effects"),
autoplot(add_no_trend, main="Additivity model without trend effects")
)
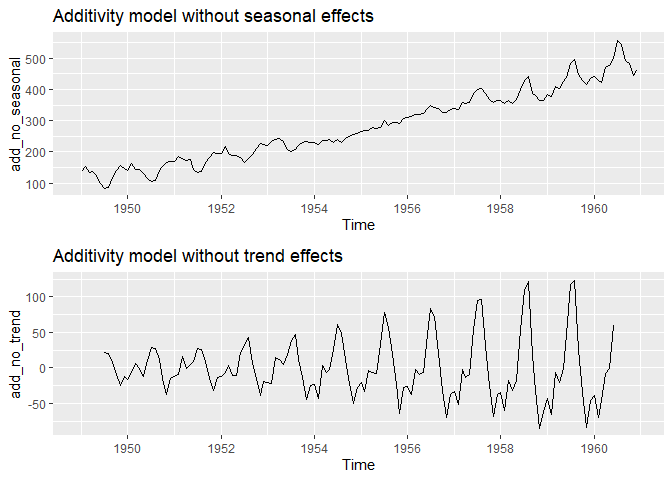
승법분해모형
승법분해모형은 계절변동이 규칙적이고 추세에 의존적인 경우 적합한 모형으로 $Y_{t}=TC_{t}\times S_{t}\times I_{t}$ 을 가정합니다. 모형을 분해하는 절차는 다음과 같습니다.
STEP1
이동평균(Moving Average)를 사용하여 추정치 $\hat{TC_{t}}$를 구합니다. 이를 $CMA_{t,d}$(시점 t에서 d개항을 이동평균)라고 합니다.
STEP2
$S_{t}*I_{t}$의 추정치 $y_{t}/\hat{TC_{t}}$를 계산합니다.
STEP3
$y_t / \hat{TC_t}$계열에 대해 계절별로 평균치 $\bar{S_{t}}$를 구한 후, 그 합이 0이 되도록 조정하여 $\hat{S_{t}}$를 구합니다. 즉, $\hat{S_{t}}=\bar{S_{t}}\times \sum_{t=1}^{d}12/\bar{S_{t}}$를 계산합니다.
STEP4
Remainder component인 $\hat{R}_t=y_t/(\hat{TC_t} \times \hat{S}_t)$를 계산합니다.
승법분해모형 역시 decompose()를 사용하여 쉽게 구할 수 있습니다.
decompose(AirPassengers, type="multiplicative") %>% autoplot()

원시계열자료에서 계절 및 추세를 제거한 그림입니다. 승법모형이기 때문에 원시계열에서 요인을 나눠야합니다.
# decomposition
mul_decompose <- decompose(AirPassengers, type="multiplicative")
# remove seasonal, trend effects
mul_no_seasonal <- AirPassengers / mul_decompose$seasonal
mul_no_trend <- AirPassengers / mul_decompose$trend
# make plot
mul_no_season_plot <- autoplot(mul_no_seasonal) +
ggtitle("Multiplicative model without seasonal effects")
mul_no_trend_plot <- autoplot(mul_no_trend) +
ggtitle("Multiplicative model without trend effects")
# output plot
grid.arrange(
mul_no_season_plot, mul_no_trend_plot
)
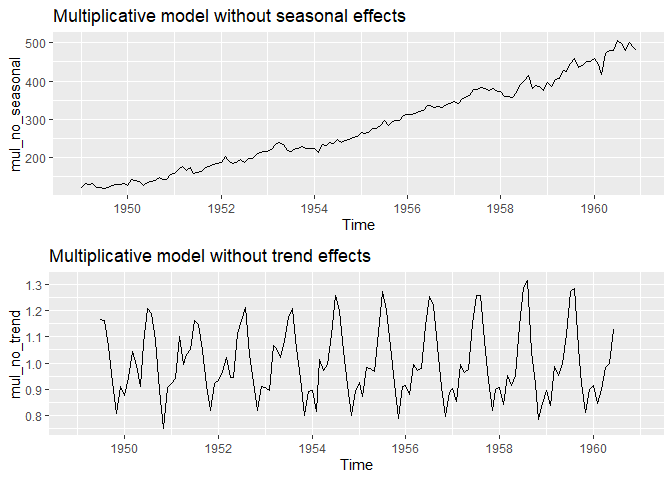
정상성 검정(stationary test)
마지막으로 remainder component가 정상성을 만족하는지 확인합니다.
#Stationary for random variation after trend and seaso
tseries::kpss.test(add_decompose$random, null = "Level")
## Warning in tseries::kpss.test(add_decompose$random, null = "Level"): p-value
## greater than printed p-value
##
## KPSS Test for Level Stationarity
##
## data: add_decompose$random
## KPSS Level = 0.016442, Truncation lag parameter = 4, p-value = 0.1
#Stationary for random variation after trend and seasona
tseries::kpss.test(mul_decompose$random, null = "Level")
## Warning in tseries::kpss.test(mul_decompose$random, null = "Level"): p-value
## greater than printed p-value
##
## KPSS Test for Level Stationarity
##
## data: mul_decompose$random
## KPSS Level = 0.033058, Truncation lag parameter = 4, p-value = 0.1
가법분해모형과 승법분해모형 모두 아주 큰 p-value를 가지는 것으로 보아, 정상성을 만족함을 알 수 있습니다. 마지막으로 remainder component의 time plot과 ACF, PACF를 출력합니다. ggplot2패키지의 ggtsdisplay()를 사용하면 깔끔한 이미지를 출력합니다.
Additive Model
ggtsdisplay(add_decompose$random, main="Random/ Additive model")

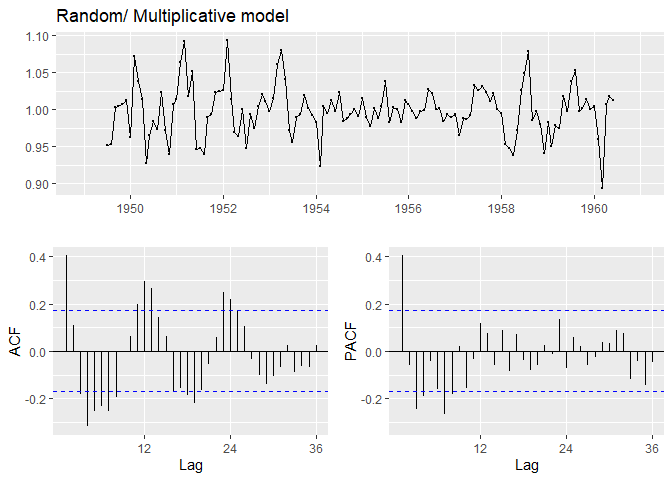
Multiplicative Model
ggtsdisplay(mul_decompose$random, main="Random/ Multiplicative model")
Classical Decomposition의 한계
Classical Decomposition은 다음과 같은 이유로 주로 사용되지는 않습니다.
- trend-cycle 요인의 처음과 마지막 몇개의 관측치를 제거해버립니다.
- trend-cycle 요인을 over-smooth하게 만듭니다.(여기서는 잘 분해 되었지만, 일부 데이터는 너무 Flexible?한 결과를 만들어냅니다.)
- 이 분해법은 계절 성분이 해마다 반복되기를 가정합니다. (예를 들어, 에어컨이 등장하기 이전에 전기소모량은 겨울에 최대수요를 가졌지만, 현재는 여름에 최대수요를 가집니다. 고전 분해법은 이러한 계절변화를 반영하지 못합니다.)
다양한 분해법들
앞서 Classical Decomposition의 단점들로 인해, 이를 대신하여 다양한 분해법들이 등장합니다. 대표적인 3가지 분해법(X11, SEATS, STL)을 R로 어떻게 구현하는지 알아봅니다.
SEATS와 X11 Decomposition
Classical Decomposition가 가지는 단점들을 보완하여 만들어졌습니다. 우선 Classical Decomposition과 달리 trend-cycle에 누락된 값을 가지지 않도록 합니다. 또한, 시간에 따른 계절요인 변화를 반영합니다. 시계열자료의 이동이나 이상치에 대해서도 robust한 성질을 가집니다. 다만, 월별이나 분기별 자료에만 적용이 가능하므로 일별 데이터, 시간별 데이터같은 경우는 다른 방법을 사용해야합니다.
R에서 seasonal패키지의 seas()함수를 사용하면 SEATS Decomposition과 X11 Decomposition을 사용할 수 있습니다. 우선 데이터의 time plot을 확인하고, Decomposition을 진행합니다.
data(elecequip)
autoplot(elecequip)
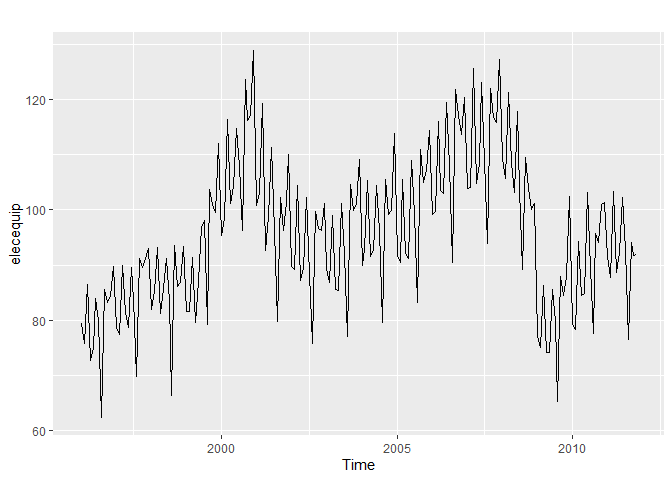
seas()에 default는 SEATS decomposition이기에, 데이터만 입력하면 SEATS를 진행합니다.
#seasonal::seas
seas(elecequip) %>%
autoplot() +
ggtitle("SEATS decomposition of electrical equipment index")
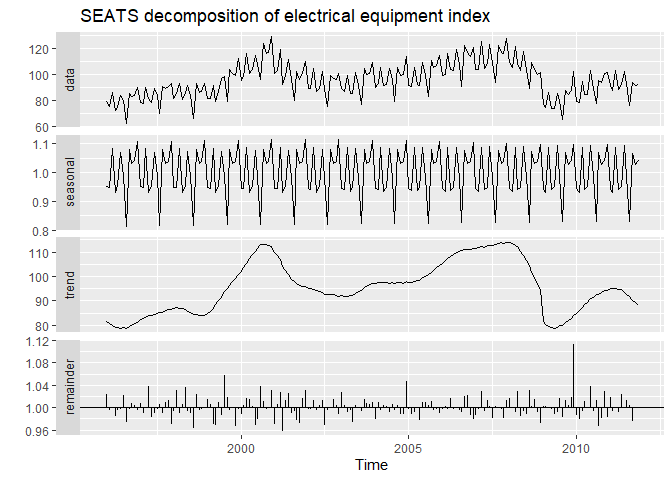
seas(X11="")을 사용하면 X11-decomposition을 사용할 수 있습니다.
fit_X11 <- elecequip %>% seas(x11="")
#A decomposition of the new orders index for electrical equipment.
autoplot(fit_X11) +
ggtitle("X11 decomposition of electrical equipment index")
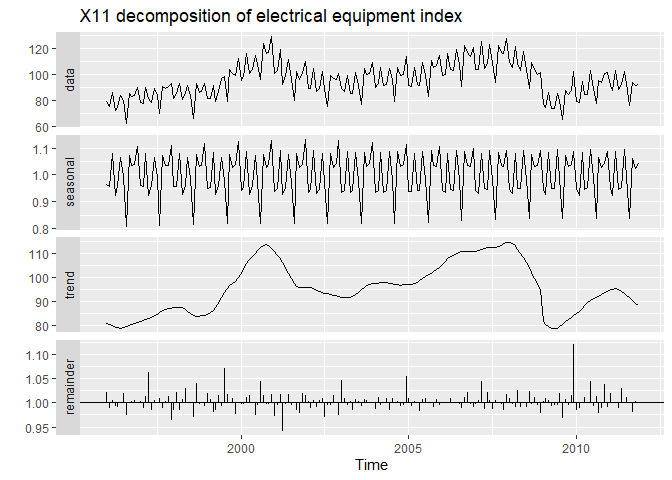
forcast패키지의 trendcycle()함수를 사용하면 추세만 뽑아낼 수 있습니다. 그 외에도 seasonal()와 remainder() 을 사용하면 각 요인들을 뽑아낼 수 있습니다. seasadj()는 seasonally adjusted time series을 계산합니다.
elecequip %>% autoplot(series="Data") +
autolayer(trendcycle(fit_X11), series="Trend") +
autolayer(seasadj(fit_X11), series="Seasonally Adjusted") +
scale_colour_manual(values=c("gray", "blue", "red"),
breaks=c("Data", "Seasonally Adjusted", "Trend")) +
xlab("Year") + ylab("New orders index") +
ggtitle("Electrical equipment manufacturing (Euro area)")
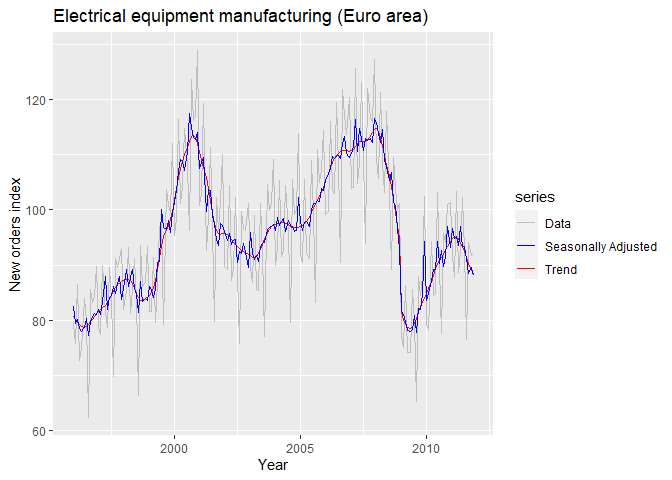
ggplot2패키지의 ggsubseriesplot()을 사용하면, sub-series plot을 그릴 수 있습니다. sub-series plot은 시간에 따른 개별 계절요소(여기서는 월별)의 변화를 시각화한 그림입니다.
fit_X11 %>% seasonal() %>% ggsubseriesplot() + ylab("Seasonal")
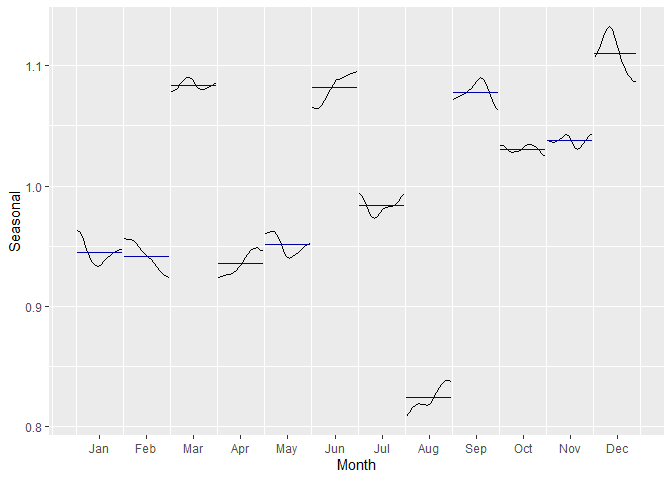
마지막으로 X11-decomposition한 데이터의 trend-cycle값들을 확인해봅니다.
fit_X11 %>% trendcycle()
#fit_X11 %>% seasonal()
#fit_X11 %>% remainder()
#fit_X11 %>% seasadj()
## Jan Feb Mar Apr May Jun Jul
## 1996 80.69206 80.21826 79.64028 79.15552 78.80442 78.67565 78.82602
## 1997 81.66166 81.98161 82.29085 82.71590 83.22066 83.83856 84.56604
## 1998 87.19999 87.38624 87.39773 87.12897 86.57215 85.76778 84.83710
## 1999 84.53125 85.03363 85.89373 87.25954 89.14995 91.33331 93.43757
## 2000 101.68364 103.81345 105.77860 107.41559 108.78674 109.96509 111.18464
## 2001 110.60215 109.12131 107.59654 105.93034 103.93652 101.67300 99.38903
## 2002 95.76579 95.55152 95.13388 94.57931 94.07525 93.70515 93.35840
## 2003 91.63771 91.38688 91.31626 91.50970 92.00312 92.75321 93.75358
## 2004 97.40030 97.51860 97.60667 97.68457 97.68341 97.54801 97.28749
## 2005 96.92109 97.12912 97.44735 97.95973 98.64121 99.46164 100.29810
## 2006 105.32100 106.58927 107.70511 108.56282 109.21568 109.76428 110.21101
## 2007 110.69642 110.98731 111.45415 111.94593 112.28188 112.34821 112.28775
## 2008 114.66977 114.18420 113.13533 111.60582 109.85561 108.08622 106.26599
## 2009 81.55544 80.22452 79.27926 78.70523 78.51121 78.70632 79.37416
## 2010 84.83880 85.77358 86.86819 88.11179 89.28367 90.25493 90.89101
## 2011 94.72582 95.02912 95.05018 94.73001 94.14723 93.34093 92.37354
## Aug Sep Oct Nov Dec
## 1996 79.22557 79.69558 80.21041 80.73628 81.23312
## 1997 85.26434 85.89531 86.40020 86.72235 86.96493
## 1998 84.06165 83.66278 83.63464 83.85684 84.16727
## 1999 95.15212 96.33018 97.21209 98.24713 99.75250
## 2000 112.34667 113.18722 113.47955 113.07298 112.00472
## 2001 97.46494 96.22518 95.67720 95.60038 95.72240
## 2002 93.00565 92.69495 92.42951 92.18984 91.93794
## 2003 94.82139 95.76901 96.47235 96.91711 97.20500
## 2004 97.02119 96.82821 96.70843 96.72900 96.81116
## 2005 101.04100 101.70081 102.35850 103.12541 104.11420
## 2006 110.54285 110.72255 110.79863 110.73869 110.63011
## 2007 112.35150 112.69862 113.26339 113.95934 114.53845
## 2008 104.20121 101.90335 99.51121 97.14660 94.91518
## 2009 80.41400 81.53681 82.50617 83.30075 84.02984
## 2010 91.35976 91.88962 92.59944 93.39884 94.15279
## 2011 91.31287 90.19764 89.16781 88.27430
Classical Decomposition과 달리, X-11 Decomposition은 처음과 마지막 값을 함께 출력합니다.
STL Decomposition
STL은 Classical, X11, SEATS Decomposition에 비해 다음과 같은 특징을 가집니다.
- SEATS, X11과 달리, STL은 월별과 분기별 이외에 여러 계절유형을 다룰 수 있습니다.
- 시간의 따른 계절요소 변화를 적용할 수 있으며, 얼만큼 변하는지 사용자가 통제할 수 있습니다.
- 이상치에 robust한 성질을 가집니다.
- smoothness of trend-cycle를 사용자가 조절할 수 있습니다.
- trading day calendar variation을 자동적으로 다루지는 못합니다.
- 가법모형만 제공하며, 승법모형을 사용하기 위해서는 Box-Cox변환을 해야합니다.
R에서 stl()함수를 사용하면, STL Decomposition을 사용할 수 있습니다. s.window는 default가 없으므로 반드시 명시해줘야합니다. 그 외에도 robust, t.window등이 있는데 자세한 내용은 ?stl로 옵션에 대한 설명을 얻을 수 있습니다. 여기서는 robust=T 유무에 따른 결과의 차이를 보겠습니다.
#stats::stl
stl_fit <- stl(elecequip, s.window="periodic")
stl_fit_robust <- stl(elecequip, s.window="periodic", robust = T)
grid.arrange(
stl_fit %>% autoplot() + ggtitle("No Robust Model"),
stl_fit_robust %>% autoplot() + ggtitle("Robust Model"),
nrow=1, ncol=2
)
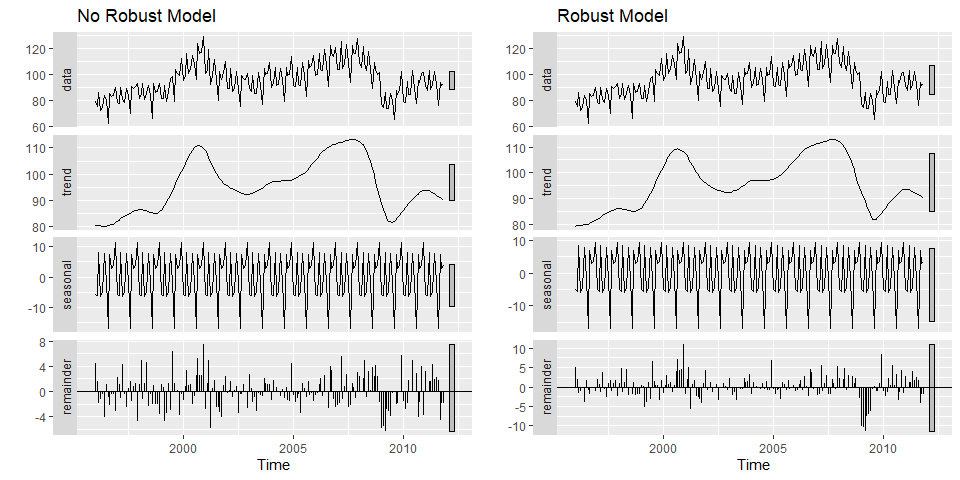
2009년에 급격히 감소하는 이상치를 가집니다. 두 모델을 비교해보면, robust=T모델이 이상치에 robust한 trend-cycle을 만들었습니다.(2009년의 remainder를 살펴보면 robust모델이 더 큰 음의 값을 가지는 것을 보면 알 수 있습니다.)
다음으로 forcast()를 사용하여 이후 24개 자료에 대한 예측을 진행합니다.
forecast_stl <- forecast::forecast(stl_fit_robust)
forecast_stl
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## Dec 2011 96.60043 92.72916 100.47170 90.67983 102.52103
## Jan 2012 81.19582 76.77071 85.62093 74.42820 87.96345
## Feb 2012 80.05010 74.86809 85.23210 72.12491 87.97529
## Mar 2012 93.52743 87.47376 99.58109 84.26915 102.78571
## Apr 2012 78.80554 71.82787 85.78321 68.13412 89.47697
## May 2012 79.76644 71.85043 87.68246 67.65995 91.87294
## Jun 2012 91.99761 83.15082 100.84440 78.46762 105.52761
## Jul 2012 82.12229 72.36447 91.88011 67.19899 97.04559
## Aug 2012 66.74844 56.10573 77.39116 50.47181 83.02507
## Sep 2012 90.61892 79.12041 102.11742 73.03347 108.20436
## Oct 2012 86.31835 73.99406 98.64265 67.46997 105.16674
## Nov 2012 86.95536 73.83497 100.07576 66.88945 107.02128
## Dec 2012 92.79427 78.90644 106.68209 71.55468 114.03386
## Jan 2013 78.15089 63.52292 92.77887 55.77934 100.52245
## Feb 2013 77.61415 62.27172 92.95658 54.14993 101.07837
## Mar 2013 91.57867 75.54584 107.61151 67.05857 116.09877
## Apr 2013 77.24654 60.54573 93.94735 51.70485 102.78822
## May 2013 78.51924 61.17132 95.86716 51.98788 105.05060
## Jun 2013 90.99985 73.02420 108.97550 63.50846 118.49124
## Jul 2013 81.32408 62.73871 99.90945 52.90021 109.74795
## Aug 2013 66.10987 46.93151 85.28823 36.77910 95.44064
## Sep 2013 90.10806 70.35227 109.86385 59.89419 120.32193
## Oct 2013 85.90967 65.59094 106.22840 54.83485 116.98449
## Nov 2013 86.62842 65.76024 107.49659 54.71329 118.54354
autoplot(forecast_stl)
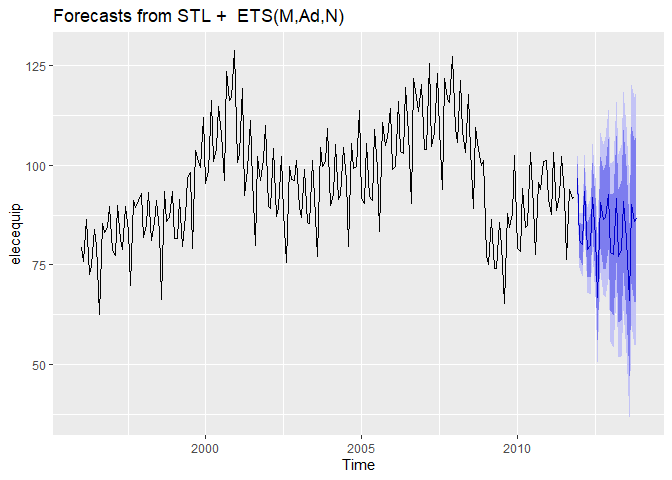
Visualization
ggplot2패키지는 시계열자료를 시각화하기위한 여러 함수들을 제공합니다. 먼저 시각화할 시계열 데이터를 불러옵니다.
data(a10)
a10 %>% head(18)
## Jan Feb Mar Apr May Jun Jul Aug
## 1991 3.526591 3.180891
## 1992 5.088335 2.814520 2.985811 3.204780 3.127578 3.270523 3.737851 3.558776
## Sep Oct Nov Dec
## 1991 3.252221 3.611003 3.565869 4.306371
## 1992 3.777202 3.924490 4.386531 5.810549
#Monthly sales of antidiabetic drugs in Australia.
autoplot(a10) +
ggtitle("Antidiabetic drug sales") +
xlab("Year") + ylab("$ million")
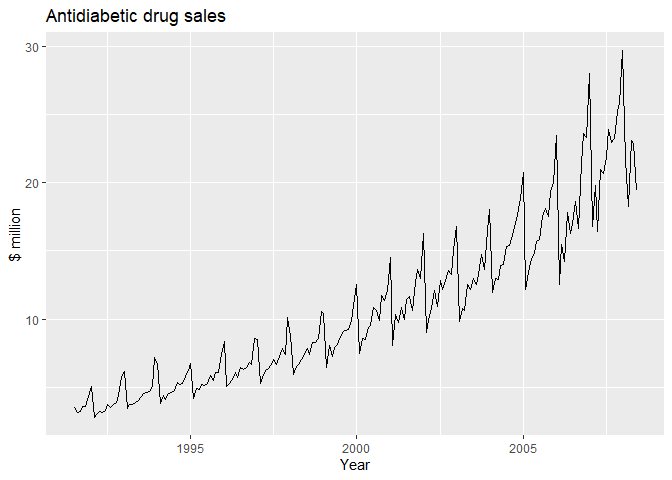
ggseasonal()을 사용하면 년도별로 계절요소(월별)에 따른 시계열 자료를 시각화할 수있습니다.
#Seasonal plot of monthly antidiabetic drug sales in Australia.
ggseasonplot(a10, year.labels=TRUE, year.labels.left=F) +
ylab("$ million") +
ggtitle("Seasonal plot: antidiabetic drug sales")
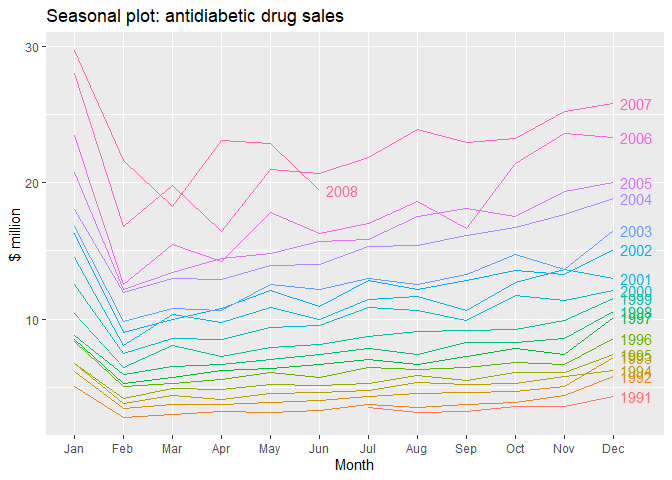
polar=TRUE 옵션을 추가해봅니다.
#Polar seasonal plot of monthly antidiabetic drug sales in Australia.
ggseasonplot(a10, polar=TRUE) +
ylab("$ million") +
ggtitle("Polar seasonal plot: antidiabetic drug sales")
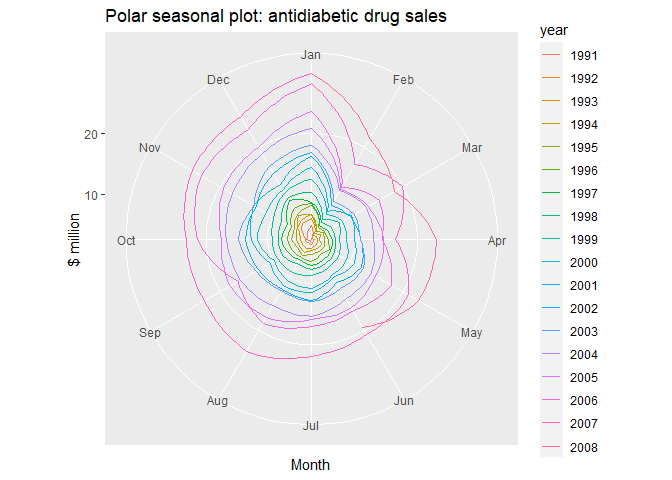
ggsubseriesplot()을 사용하여 sub-series plot을 그립니다.
#Seasonal subseries plot of monthly antidiabetic drug sales in Australia.
ggsubseriesplot(a10) +
ylab("$ million") +
ggtitle("Seasonal subseries plot: antidiabetic drug sales")
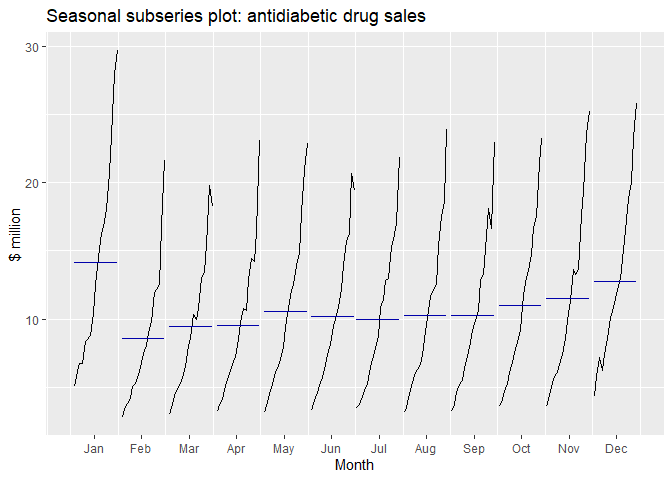
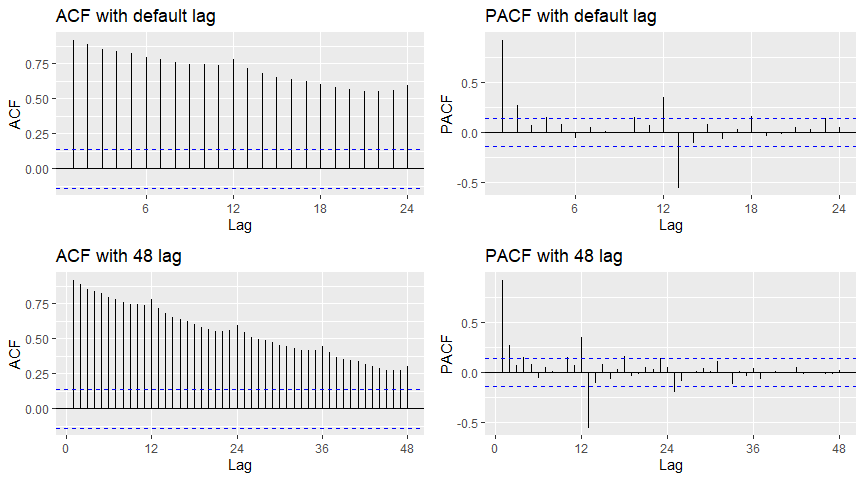
ggAcf()와 ggPacf()를 사용하여 Acf와 Pacf를 시각화할 수 있습니다.
# ACF
grid.arrange(
ggAcf(a10) + ggtitle("ACF with default lag"),
ggPacf(a10) + ggtitle("PACF with default lag"),
ggAcf(a10, lag=48) + ggtitle("ACF with 48 lag"),
ggPacf(a10, lag=48) + ggtitle("PACF with 48 lag"),
nrow=2, ncol=2
)

Leave a comment